引言

函数是数学中最基本的概念之一，它在各个领域都有广泛的应用。函数的性质是研究函数行为的关键，它帮助我们理解函数在不同条件下的表现。本文将探讨函数性质的几个重要方面，包括函数的定义域、值域、奇偶性、周期性以及连续性和可导性等。

函数的定义域和值域

函数的定义域是指函数可以接受的所有输入值的集合，而值域则是函数输出值的集合。了解函数的定义域和值域对于理解函数的整体行为至关重要。

定义域可以通过以下几种方式确定：

• 直接从函数表达式分析，例如，分母不为零、根号内非负等。
• 考虑函数的实际应用背景，例如，物理量的取值范围。
• 结合图形直观判断，观察函数图像的横坐标范围。

值域可以通过以下几种方式确定：

• 直接从函数表达式分析，例如，指数函数的值域为正实数。
• 利用函数的奇偶性和周期性进行推导。
• 结合图形直观判断，观察函数图像的纵坐标范围。

函数的奇偶性

函数的奇偶性是描述函数对称性的重要性质。一个函数可以是奇函数、偶函数或都不是。

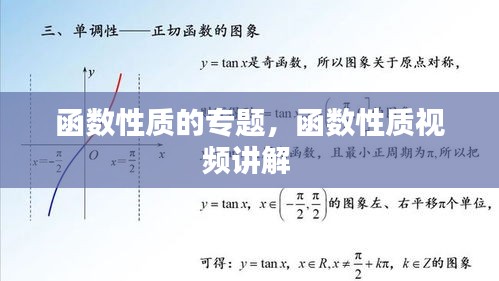
奇函数满足条件 f(-x) = -f(x)，其图像关于原点对称。偶函数满足条件 f(-x) = f(x)，其图像关于y轴对称。如果一个函数既不满足奇函数的条件也不满足偶函数的条件，则称其为非奇非偶函数。

奇偶性的判断方法包括：

• 直接代入-x，比较f(-x)与f(x)的关系。
• 利用函数的对称性，通过图形直观判断。

函数的周期性

周期性是描述函数在特定间隔内重复其行为的性质。一个函数如果存在一个非零实数T，使得对于所有x，都有f(x + T) = f(x)，则称该函数是周期函数，T称为周期。

周期函数的判断方法包括：

• 观察函数图像的重复模式。
• 通过代数方法推导周期性，例如，利用函数的导数和积分。

函数的连续性和可导性

函数的连续性和可导性是描述函数在特定点附近变化趋势的重要性质。

连续性是指函数在某一点的极限存在且等于该点的函数值。一个函数在其定义域内连续，意味着该函数在该区间内没有间断点。

可导性是指函数在某一点的导数存在。导数描述了函数在该点附近的斜率，是函数变化速率的度量。

连续性和可导性的判断方法包括：

• 利用极限的定义判断连续性。
• 利用导数的定义判断可导性。
• 结合图形直观判断，观察函数图像的平滑程度。

结论

函数性质的专题研究对于深入理解函数的行为和应用具有重要意义。通过对定义域、值域、奇偶性、周期性、连续性和可导性的探讨，我们可以更好地把握函数的本质，为解决实际问题提供理论支持。

在数学学习和应用中，不断深化对函数性质的理解，有助于我们更好地运用函数这一工具，为科学研究、工程实践和社会发展贡献力量。